Close packing means that if assuming hard sphere model for atoms, we would have as much dense packing of those hard spheres as possible. Specifically, this refers to the packing of equal spheres (radius being equal). Normally, we have two types of close packing, the hexagonal close packing (HCP) and face-centered cubic (FCC) type of packing. As shown in the picture below,
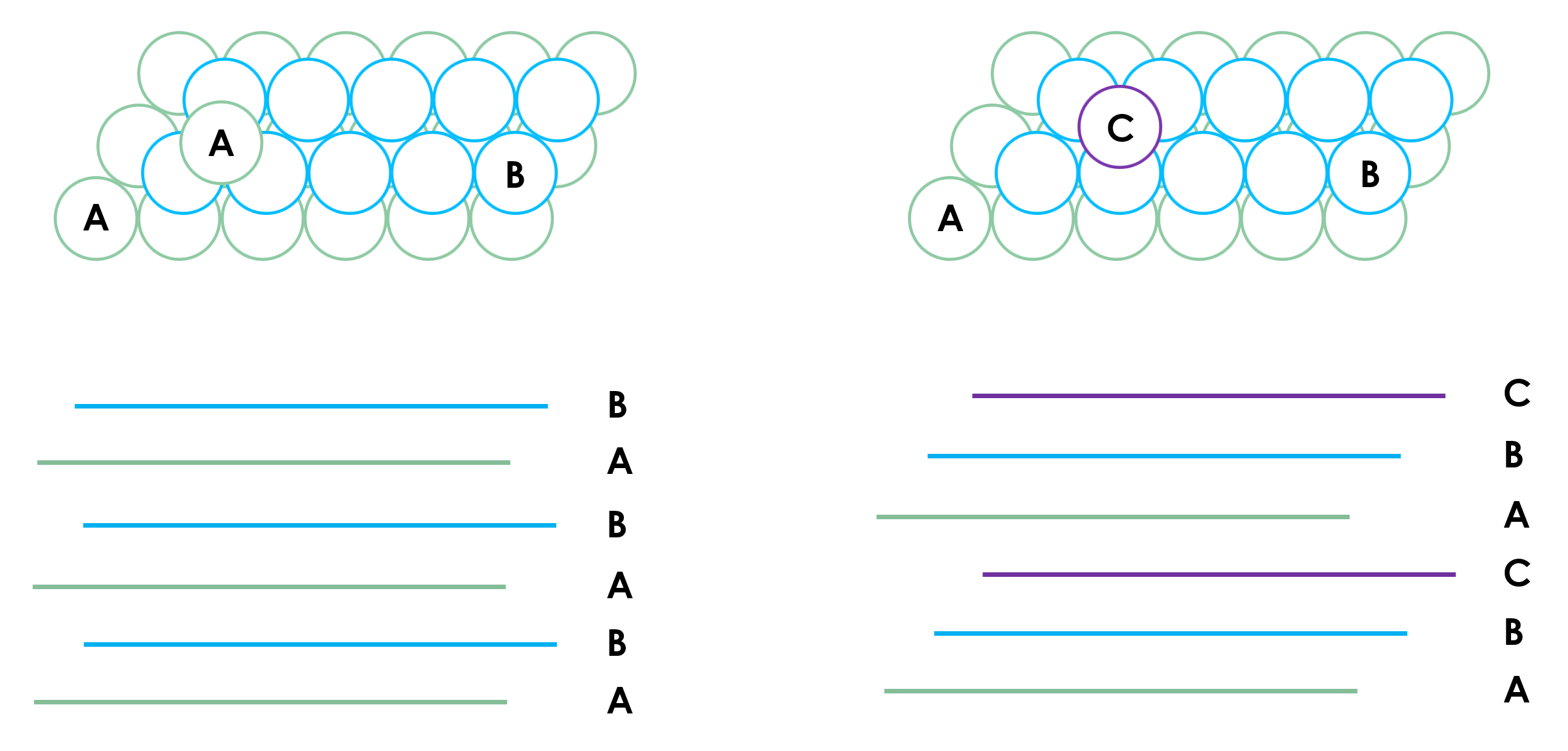
once we lay down the first layer of atoms (the green ones in the bottom layer), there is only one way to lay down the second layer of atoms on top of the first layer, by filling the space formed by the first layer of atoms. Further, there are two choices for the third layer - either we fill the space in such a way that all atoms in the third layer are straightly above an atom in the first layer, which is the case shown on the left side, i.e., the ABAB... type of stacking, which is the HCP stacking, or we can have atoms in the third layer filling up the spaces that are not straightly above the first layer of atoms, to form the ABCABC... type of stacking, which is the FCC stacking.
Either of the two types of stacking alone will form a perfect crystal in which the specific type of stacking sequence will repeat itself infinitely. However, in practice, we all know that we will always have imperfections in the crystal. Concerning the stacking sequence, it is possible, for example, that among the ABCABC... type of sequence, we could have local ‘glitch’ where the sequence temporarily changes to ABAB type, as shown in the picture below,
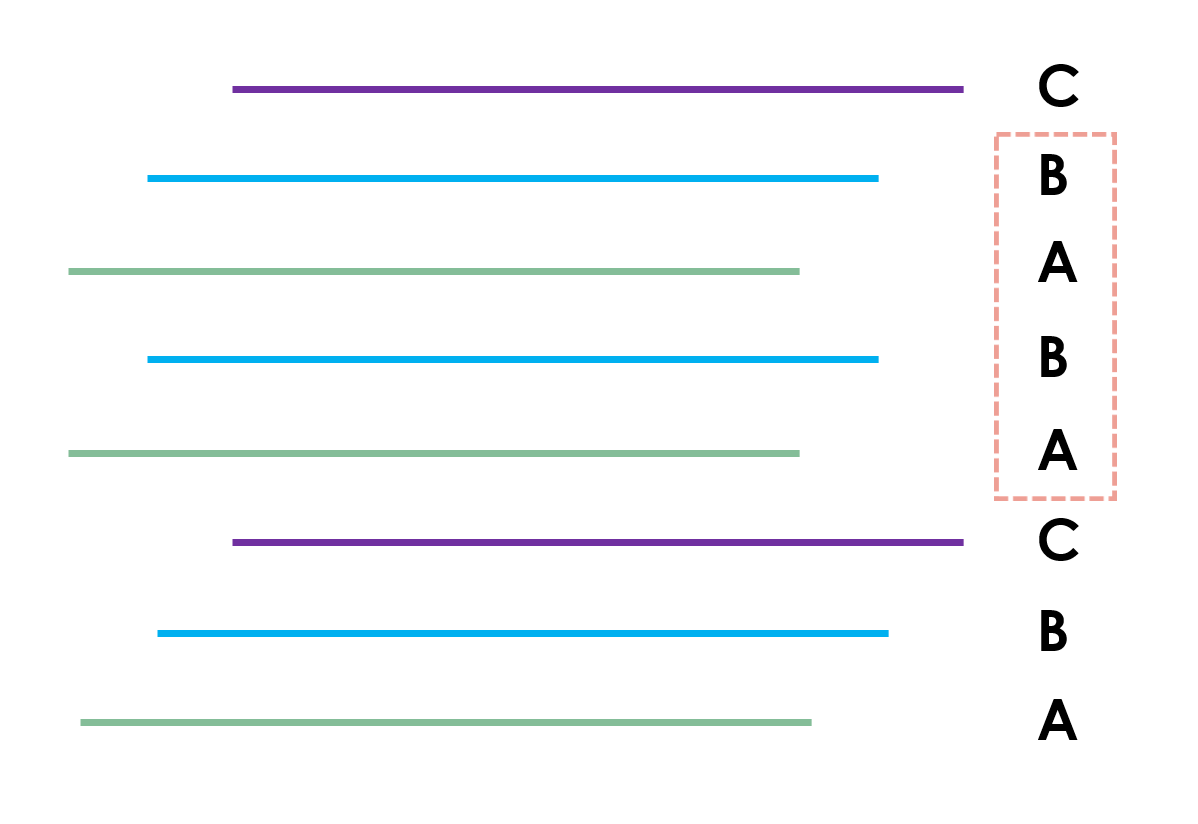
This is what we mean by stacking faults. We can imagine that the perfect stacking sequence would yield a certain lattice whereas if we have stacking faults, the imperfection in the sequence would then break the normal periodicity and thus would induce corresponding features in the diffraction pattern. For the formation of stacking faults and other relevant general information, refer to the very interesting resource by H. Foll in Ref. [1].