In one of my previous posts, I had some notes about the preferred orientation and texture and the two typical ways to represent them [1]. In this post, I am trying to put down some follow-up notes about the topic, hoping to add some more understanding of the topic.
Preferred orientation or texture, either one, means that we have a non-uniform distribution of those crystalline regions/domains. This is the fundamental physics. For practical life, we need some way to represent such fundamental physics, either using some functions or plots. The latter one (i.e., the plot) is what the pole figure and inverse pole figure is for. For the pole figure, refer to the figure below,
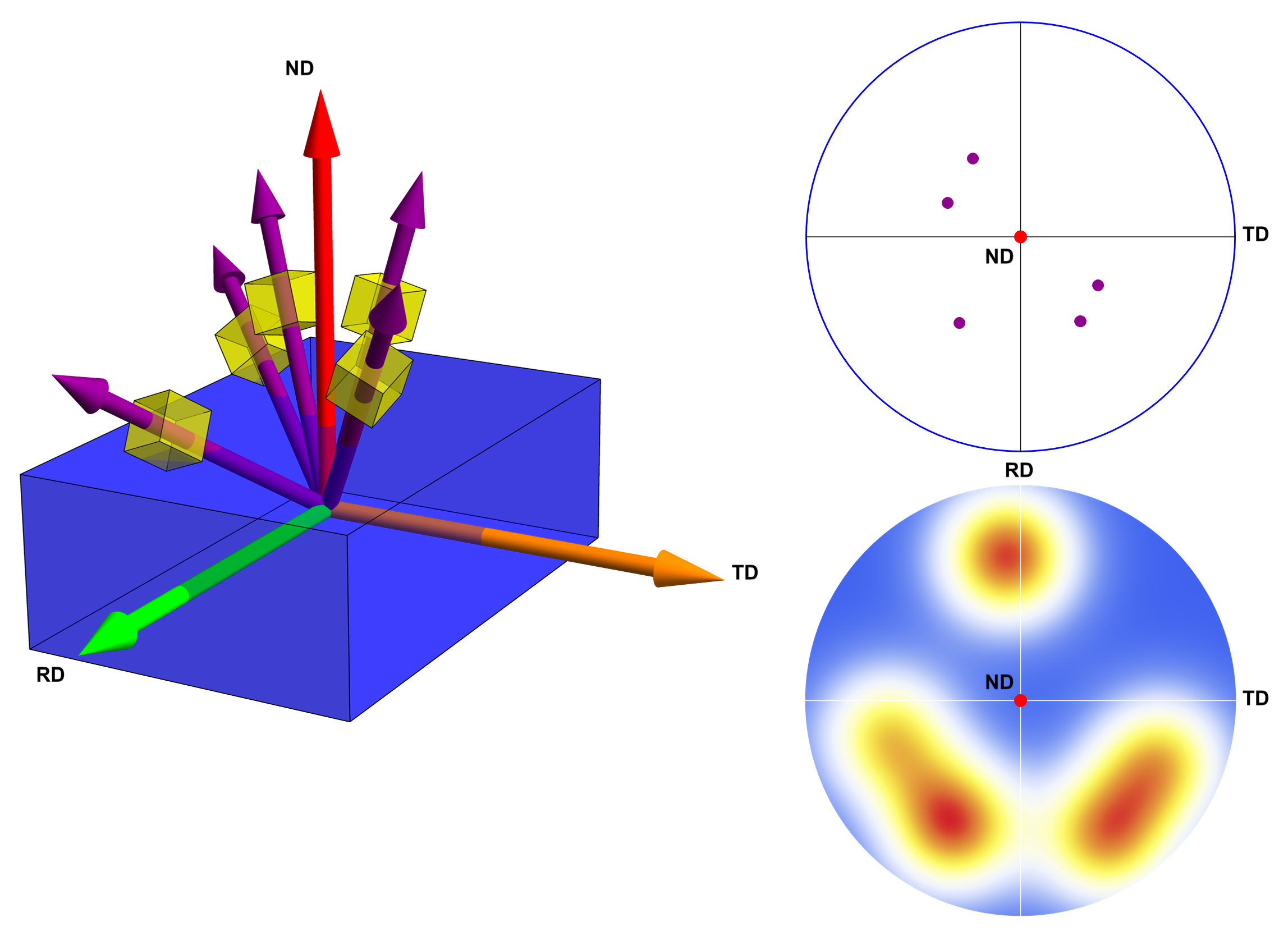
The blue cuboid represents the sample where three directions are defined, namely normal direction (ND), rolling direction (RD) and transverse direction (TD). Those magenta arrows represent the orientation of different crystallites. The direction of those arrows could be, say, the crystallographic [001] direction. So we can see that with respect to the sample reference system (defined by ND, etc.), the orientation of those crystallites are distributed. In practice, pole figure is used to represent such a distribution, and it is projected onto a 2D plane. What we do is to look towards the ND direction (the arrow points to our eyes) and project those magenta arrows to a plane perpendicular to the ND direction. The top-right image shows the result of such a projection where each magenta arrow becomes a point in the projection plane. Further, if we many of those crystallites orienting differently, we will have a continuous distribution and when projected onto the plane, we have the heat map distribution as shown in the bottom-left image. This is just the pole figure, e.g., for the [001] crystallographic direction.
With the pole figure, we can get a feel about the distribution of the crystallites orientation but it is not the full picture. For example, if we take any of the yellow cubes (representing a certain crystallite) and we again assume that the magenta arrow represents the [001] direction of the crystal. Then having the [001] direction pointing along the magenta arrow direction, we can have the crystal rotating around the magenta arrow direction for any angle so that the [001] direction of the crystal still points along the magenta arrow direction. Therefore, independent from such an arbitrary rotation, although the orientation of the crystal changes, the corresponding [001] pole figure will not change at all. Going beyond, we have the Orientation Distribution Function (ODF). Again, taking any of the yellow cube as an example, if we agree upon a set of orthogonal crystallographic directions as the crystallographic coordinate system, we can rotate the sample reference system in a certain manner (through, e.g., three Euler angles – see Ref. [2] for a nice demonstration) to match the crystallographic directions. Then the distribution of crystallites orientation will be come the distribution over the three Euler angles. Here below I am showing an illustration figure for the ODF,
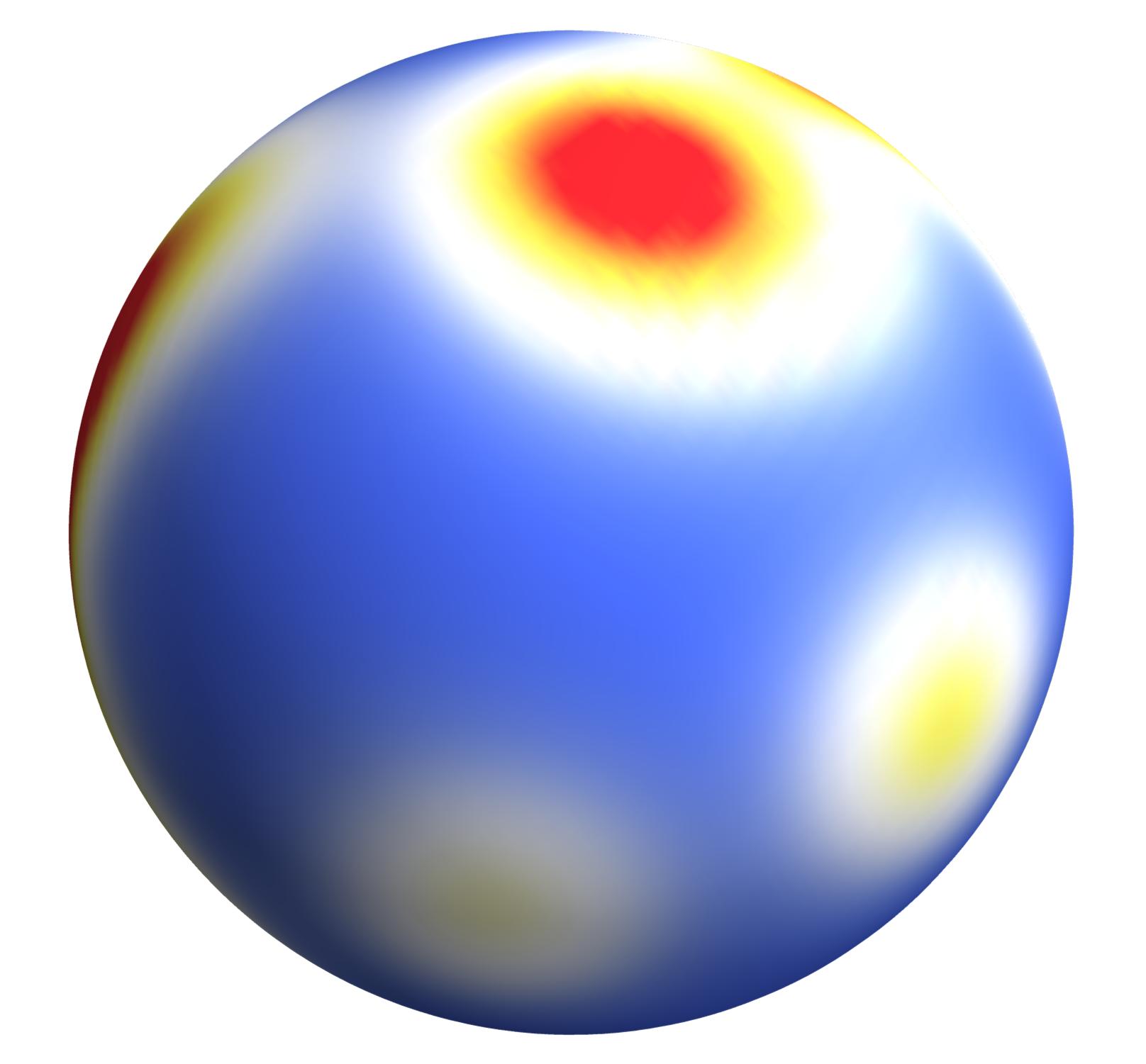
Each point on the sphere surface represents a certain crystallite orientation – a certain set of Euler angles is associated with a point on the surface and such a set of Euler angles is the angles that the sample reference coordinate system (the ND, RD and TD directions) takes to rotate to the crystallographic coordinate system. The color represents the probability density – those ‘hot spots’ on the surface means we have higher probability to find crystallites orienting in a certain way. Fundamentally, the ODF and pole figures are associated with each other. Going from the ODF to pole figures is relatively straightforward but going the other way round is not as so. It is beyond the scope of this post and my capacity to comprehend the details about the construction of the PDF from multiple pole figures. Details can be found in Ref. [3] (see Chapter 3).
In Ref. [4], I include some Mathematica files with which I generated the figures used in the current post.
References
[1] Preferred Orientation and Texture
[2] https://www.doitpoms.ac.uk/tlplib/crystallographic_texture/codf.php
[4] Useful utilities