
In this article, I am going to note down my bits of understanding for the role that Fourier transform is playing in total scattering regime. Quite often we hear people talking about real space or reciprocal space representation of the total scattering signal. Also, it’s probably a common sense that the two spaces are coupled by Fourier transform. But if pulling ourselves out of those technical details for the moment and think about why Fourier transform comes into play in total scattering regime in the first place, sometimes we may find ourselves in a situation like ‘um…but…why?’
Before diving into the specific total scattering topic, I will first mention a little bit background about Fourier transform. Here I will not try to reproduce details about it from head to toe, since obviously a simple Googling will guide us to tons of available resources about such a topic. Therefore, there is no need at all to reinvent the wheel. Instead, I will pick up a very interesting visualization of Fourier transform that I came across on YouTube and try to reproduce it here as an intro before going into my topic. Also, I will recover two little pieces of problems that I encountered during learning total scattering. They are not crucial for understanding the topic but I think it’s always good to stop and think why, instead of just accepting them as being granted.
So, first lets start with the visualization of Fourier transform mentioned above. As I said, I first came across this fantastic visualization in a YouTube video, which one can check out here: Click Me! The original post can be found in the blog titled Purrier Series (Meow) and Making Images Speak, in which Mathematica was used to generate those fabulous animations. Also, mathematical formulation can be found either in the post mentioned here or the link here: Click Me! Here, I took the same idea and make a simple reproduction of two simple animations with Python, just as a practice. What we are transforming here is a square function and only the first two components are considered here. The transformation involving only the first component is like this:
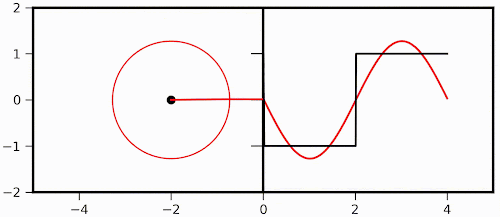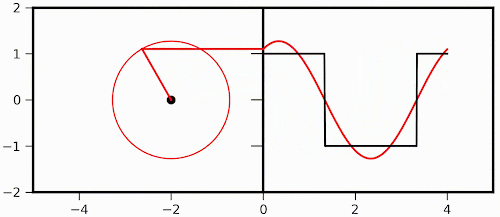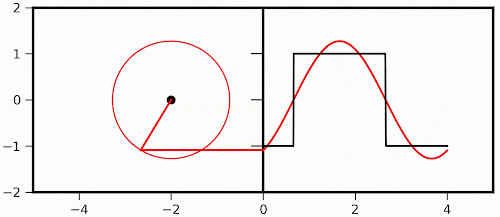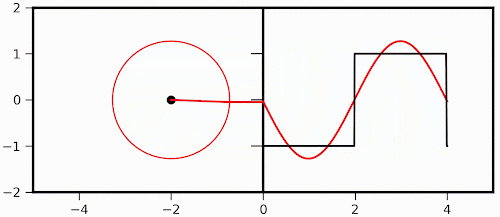
Then the first and third components are involved:
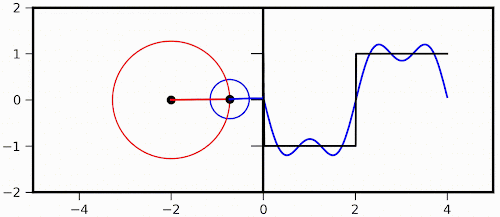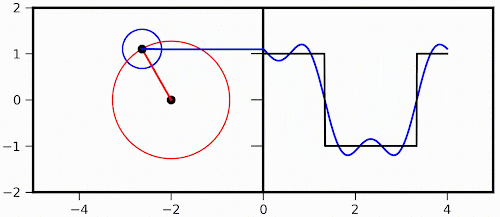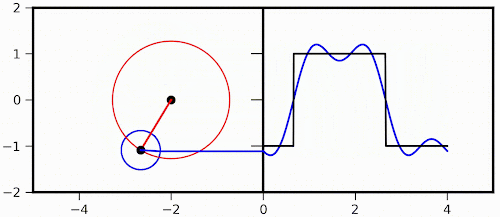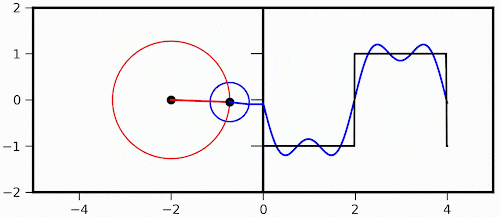
The Python script used to generate the two animations above is reproduced as follows (one needs numpy and matplotlib to run it):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 | import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation # Function to be used as the updator for first Fourier component. # Here we have, # 'line' for rotating bar # 'line1' for scanning bar moving up and down # 'line2' for plotting the first Fourier component. # 'line3' for plotting the original square function. def update_line_1(num, xy_plot, line, line1, line2, line3): line.set_data([-2, xy_plot[num - 1][0]], [0, xy_plot[num - 1][1]]) line1.set_data([xy_plot[num - 1][0], 0], [xy_plot[num - 1][1], xy_plot[num - 1][1]]) # x2_temp = [item[0] for item in xy1_plot[:num]] # y2_temp = [item[1] for item in xy1_plot[:num]] x2_temp = [item[0] for item in xy1_plot[num]] y2_temp = [item[1] for item in xy1_plot[num]] line2.set_data(x2_temp, y2_temp) x2_temp = [item[0] for item in xy_line_plot[num]] y2_temp = [item[1] for item in xy_line_plot[num]] line3.set_data(x2_temp, y2_temp) return line, line1, line2, line3 # Function to be used as the updator for first and third Furier component. # Here we have, # 'line' for rotating bar indicating the first component. # 'line1' for scanning bar moving up and down. # 'line2' for plotting the first and third Fourier components. # 'patch1' for rotating circle indicating the third component. # 'line3' for the center of the rotating circle (again, indicating the # third component). # 'line4' for the rotating bar indicating the third component. # 'line5' for plotting the original square function. def update_line_3(num, xy_plot, line, line1, line2, patch1, line3, line4, line5): line.set_data([-2, xy_plot[num - 1][0]], [0, xy_plot[num - 1][1]]) line1.set_data([xy_plot_1[num - 1][0], 0], [xy_plot_1[num - 1][1], xy_plot_1[num - 1][1]]) x2_temp = [item[0] for item in xy3_plot[num]] y2_temp = [item[1] for item in xy3_plot[num]] line2.set_data(x2_temp, y2_temp) patch1.center = (xy_plot[num - 1][0], xy_plot[num - 1][1]) patch1.radius = 4.0 / 3.0 / np.pi ax2.add_patch(patch1) line3.set_data([xy_plot[num - 1][0]], [xy_plot[num - 1][1]]) line4.set_data([xy_plot[num - 1][0], xy_plot_1[num - 1][0]], [xy_plot[num - 1][1], xy_plot_1[num - 1][1]]) x2_temp = [item[0] for item in xy_line_plot[num]] y2_temp = [item[1] for item in xy_line_plot[num]] line5.set_data(x2_temp, y2_temp) return line, line1, line2, patch1, line3, line4, line5 fig1, ax1 = plt.subplots() ax1.set_aspect('equal') ax1.spines["bottom"].set_linewidth(2) ax1.spines["top"].set_linewidth(2) ax1.spines["left"].set_linewidth(2) ax1.spines["right"].set_linewidth(2) ax1.tick_params(direction='out', length=6) # The static circle indicating the first component. circle = plt.Circle((-2, 0), 4 / np.pi, color='red', fill=False) ax1.add_artist(circle) # The rotating circle indicating the third component. patch1 = plt.Circle((0, 0), 0.0, fc='y') # Plot some indicator ticks for the graph. plt.plot(-2, 0, '-o', color='gray', markersize=5, linewidth=4, markerfacecolor='black', markeredgecolor='black', markeredgewidth=2) plt.plot([0, 0], [-2, 2], '-', color='black', markersize=5, linewidth=2, markerfacecolor='black', markeredgecolor='black', markeredgewidth=2) plt.plot([-0.25, 0], [0, 0], '-', color='black', markersize=5, linewidth=1, markerfacecolor='black', markeredgecolor='black', markeredgewidth=2) plt.plot([-0.25, 0], [1, 1], '-', color='black', markersize=5, linewidth=1, markerfacecolor='black', markeredgecolor='black', markeredgewidth=2) plt.plot([-0.25, 0], [-1, -1], '-', color='black', markersize=5, linewidth=1, markerfacecolor='black', markeredgecolor='black', markeredgewidth=2) # Generating data for plotting. x_temp = np.linspace(0, 4.0, 500) # First, the rotating bar indicating the first component. xy_plot = [] for i in range(len(x_temp)): xy_plot.append([4.0 / np.pi * np.cos(np.pi / 2.0 * x_temp[i]) - 2.0, 4.0 / np.pi * np.sin(np.pi / 2.0 * x_temp[i])]) # Then, the rotating bar indicating the third component. For this one, # the origin is rotating as well. xy_plot_1 = [] for i in range(len(x_temp)): center_1 = [-2.0, 0] center_2 = [4.0 / np.pi * np.cos(np.pi / 2.0 * x_temp[i]), 4.0 / np.pi * np.sin(np.pi / 2.0 * x_temp[i])] ending = [4.0 / np.pi / 3.0 * np.cos(3.0 * np.pi / 2.0 * x_temp[i]), 4.0 / np.pi / 3.0 * np.sin(3.0 * np.pi / 2.0 * x_temp[i])] xy_plot_1.append([center_1[0] + center_2[0] + ending[0], center_1[1] + center_2[1] + ending[1]]) # Moving square function. xy_line_plot = [] for i in range(len(x_temp)): xy_line_plot.append([]) for j in range(len(x_temp)): t_part = np.pi / 2.0 * x_temp[i] x_part = np.pi / 2.0 * x_temp[j] y_temp = np.sign(np.sin(t_part - x_part)) xy_line_plot[i].append([x_temp[j], y_temp]) # Function of the first component. xy1_plot = [] for i in range(len(x_temp)): xy1_plot.append([]) for j in range(len(x_temp)): t_part = np.pi / 2.0 * x_temp[i] x_part = np.pi / 2.0 * x_temp[j] y_temp = 4 / np.pi * np.sin(t_part - x_part) xy1_plot[i].append([x_temp[j], y_temp]) # Function of the third component. xy3_plot = [] for i in range(len(x_temp)): xy3_plot.append([]) for j in range(len(x_temp)): t_part_1 = np.pi / 2.0 * x_temp[i] x_part_1 = np.pi / 2.0 * x_temp[j] t_part_3 = 3.0 * np.pi / 2.0 * x_temp[i] x_part_3 = 3.0 * np.pi / 2.0 * x_temp[j] y_temp_1 = 4 / np.pi * np.sin(t_part_1 - x_part_1) y_temp_2 = 4.0 / np.pi / 3.0 * np.sin(t_part_3 - x_part_3) xy3_plot[i].append([x_temp[j], y_temp_1 + y_temp_2]) # Initialize and update the animation. First, we include only first # Fourier component. l, = plt.plot([], [], 'r-') l1, = plt.plot([], [], 'r-') l2, = plt.plot([], [], 'r-') l3, = plt.plot([], [], 'k-') plt.xlim(-5, 5) plt.ylim(-2, 2) line_ani_1 = animation.FuncAnimation(fig1, update_line_1, 500, fargs=(xy_plot, l, l1, l2, l3), interval=5, blit=True) # Then we add in the third component (the components of even number # are all 0). fig2, ax2 = plt.subplots() ax2.set_aspect('equal') ax2.spines["bottom"].set_linewidth(2) ax2.spines["top"].set_linewidth(2) ax2.spines["left"].set_linewidth(2) ax2.spines["right"].set_linewidth(2) ax2.tick_params(direction='out', length=6) circle = plt.Circle((-2, 0), 4 / np.pi, color='red', fill=False) ax2.add_artist(circle) patch1 = plt.Circle((0, 0), 0.0, color='blue', fill=False) # Plot some indicator ticks for the graph. plt.plot(-2, 0, '-o', color='gray', markersize=5, linewidth=2, markerfacecolor='black', markeredgecolor='black', markeredgewidth=2) plt.plot([0, 0], [-2, 2], '-', color='black', markersize=5, linewidth=2, markerfacecolor='black', markeredgecolor='black', markeredgewidth=2) plt.plot([-0.25, 0], [0, 0], '-', color='black', markersize=5, linewidth=1, markerfacecolor='black', markeredgecolor='black', markeredgewidth=2) plt.plot([-0.25, 0], [1, 1], '-', color='black', markersize=5, linewidth=1, markerfacecolor='black', markeredgecolor='black', markeredgewidth=2) plt.plot([-0.25, 0], [-1, -1], '-', color='black', markersize=5, linewidth=1, markerfacecolor='black', markeredgecolor='black', markeredgewidth=2) l, = plt.plot([], [], 'r-') l1, = plt.plot([], [], 'b-') l2, = plt.plot([], [], 'b-') l3, = plt.plot([], [], '-o', color='gray', markersize=5, linewidth=2, markerfacecolor='black', markeredgecolor='black', markeredgewidth=2) l4, = plt.plot([], [], 'b-') l5, = plt.plot([], [], 'k-') plt.xlim(-5, 5) plt.ylim(-2, 2) line_ani_3 = animation.FuncAnimation(fig2, update_line_3, 500, fargs=(xy_plot, l, l1, l2, patch1, l3, l4, l5), interval=5, blit=True) # Save the animation to movie file. For some reason, saving to # GIF file won't allow us to change the FPS and the whole animation # will become very slow. Therefore, we save the animation first as # MP4 file and use the online converter to transform to GIF file: # https://ezgif.com/ line_ani_1.save('first_component.mp4', fps=250, dpi=300) line_ani_3.save('third_component.mp4', fps=250, dpi=300) plt.show() |
Next, I will briefly talk about the two problems about Fourier transform that I mentioned earlier.
📌The \(1/2\pi\) factor appearing in the inverse Fourier transform
Usually, the Fourier transform of function \(f(x)\) is defined as,
The inverse Fourier transform will then be symmetrically and nicely given as,
\[f(x) = \int_{-\infty}^{\infty}F(f)e^{2\pi i xf}df\]according to the Fourier inversion theorem. However, quite often we will see an extra factor \(1/2\pi\) in front of the inverse Fourier transform. So the natural question is - why do we have an extra factor there? Why do we not stay with the nice and symmetric form of forward and inverse Fourier transform? The reason is simply due to the using of angular frequency (\(\omega\)) instead of frequency (\(f\)) as the independent variable in Fourier space. The relation between these two variables is simply,
\[\omega = 2\pi f\]Using \(\omega\) as our Fourier space variable, one has the forward Fourier transform as,
\[\hat{F}(\omega) = F(\frac{\omega}{2\pi}) = \int_{-\infty}^{\infty}f(x)e^{-i\omega x}dx\]where the symbol \(\hat{F}\) is used to represent the functional form with \(\omega\) as the independent variable, in contrast to the symbol \(F\) with \(f\) as the independent variable. Accordingly, the inverse Fourier transform will be given as,
\[f(x) = \int_{-\infty}^{\infty}F(f)e^{2\pi i xf}df = \int_{-\infty}^{\infty}\hat{F}(\omega)e^{ix\omega}d(\frac{\omega}{2\pi}) = \frac{1}{2\pi}\int_{-\infty}^{\infty}\hat{F}(\omega)e^{ix\omega}d\omega\]
from which one can clearly see the popping up of the extra factor \(1/2\pi\).
📌Discrete Fourier transform
The definition of Fourier transform given above is in its continuous format, whereas in practice the signal we hold in hand will never be continuous. Unlike the continuous version of Fourier transform (of which the definition is unique, as given above), we need to first pin down what we really mean by discrete Fourier transform. Suppose we have a series of data measured to be (0.1, 100), (0.12, 101), (0.15, 300), (0.16, 321), …, where the first number in each pair represents our variable (say, time \(t\)) and the second one is our response (say, voltage \(V\)), then how do we proceed to do the Fourier transform? This is where the definition of discrete Fourier transform is introduced. According to Wikipedia, we have,
in mathematics, the discrete Fourier transform (DFT) converts a finite sequence of
equally-spaced samplesof a function intoa same-length sequence of equally-spaced samples…
Therefore, for the example given above (and also in the case of total scattering as we will see later), one needs to first group the measured data into bins with equal width and then carry out the discrete Fourier transform as defined (see, e. g., Wikipedia for the exact definition).
========================I AM A SEPARATOR========================
Finishing the preparation work, we now move on to discuss the reflection of Fourier transform in total scattering regime. First of all, what is total scattering? Scattering is scattering, but what do we mean by ‘total’? Does it mean that not mentioning ‘total’ in the context indicates we are missing something? The answer is YES. But what do we miss?
In terms of scattering experiment, either with X-ray, neutron or electron, what we usually mean by ‘scattering’ is actually the Bragg reflection, in which we are specially concerned about the reflection from atom planes. The underlying rule is the famous Bragg’s law,
The common approach for analyzing Bragg pattern then focuses on the positions and intensities of those reflection peaks, which is fundamentally determined by atomic structure of material under radiation beam. Structures extracted in such a way is what we usually call as average structure. To go beyond the Bragg reflection and talk about total scattering, we need to dig into the base level of the scattering event. We already know that Bragg reflection originates from the scattering from atom planes. This is fundamentally owing to the in-phase reflection of the incoming beam from group (certain lattice plane) of atoms, leading to the overall enhanced interference effect. In that sense (and also in fact), the scattering event actually happens on the atomic level (to be more precise, X-ray interacts with electrons surrounding atoms, neutron interacts with nuclei, electron’s interaction with materials being complicated). Accordingly, the normalized (over all \(N\) atoms in the system) scattering intensity is given as,
\[\frac{1}{N}\frac{d\sigma}{d\Omega} = \frac{1}{N}\sum_{j,k}b_jb_kexp[i\mathbf{Q}\cdot(\mathbf{r}_j - \mathbf{r}_k)]\]
with the dimension of area (\(\sigma\) for cross section, \(\Omega\) for solid angle, \(b\) for scattering length (form factor in the case of X-ray scattering), \(\mathbf{Q}\) for scattering vector, \(\mathbf{r}\) for atomic position). Given the incoming flux of incoming beam (e. g. number of neutrons) per area, the product is equal to the flux of scattered beam per solid angle, which can then be equated to the experimental measurement. From the formulation given right above, one can see that the Bragg peak positions are only some special points in reciprocal space (i. e. \(Q\)-space). When only focusing on those special points in \(Q\)-space and ignoring all the other \(Q\) points (in practice, all the points other than those special ones are treated as background, in, e. g Rietveld refinement), no doubt one will lose a lot of useful information from the scattering measurement! By bringing back those ignored \(Q\) points, we will have the total scattering pattern, enabling us to retrieve those missing information - the local structure - in conventional Bragg data analysis. This is where Fourier transform comes to play an important role, which is what we will cover right next.
For the following discussion, we refer ourselves to the book by M. Dove [1] (see Appendix-J in the book for detailed derivations), with several key aspects recovered in current context. First, by pulling out all the self-terms, one arrives at,
in which \(F(Q)\) can be further expressed as,
\[F(Q) = \rho\sum_{j,k}c_jc_kb_jb_k4\pi\int_{0}^{\infty}r^2g_{jk}(r)\frac{sin(Qr)}{Qr}dr\]where \(c\) represents the proportion of atoms of each type, \(\rho\) refers to the overall number density of the system, and the term \(sin(Qr)/Qr\) comes from the isotropic orientational average of \(\langle exp[i\mathbf{Q}\cdot(\mathbf{r}_j - \mathbf{r}_k)]\rangle\). It’s worth mentioning that the following part in the definition of \(F(Q)\) gives the average number of atoms of type \(k\) within the shell \(r\rightarrow r+dr\) surrounding atoms of type \(j\),
\[\rho c_k4\pi r^2g_{jk}(r)dr\]
while \(c_j\) in the definition of \(F(Q)\) fundamentally comes from the normalization over the total number of atoms (\(N\)) in the system. The logic here is that we treat all inter-atomic distances within the range \(r\rightarrow r+dr\) to be the same and we count the number of atomic pairs with such a distance and multiply that number to the phase factor (in this case, \(sin(Qr)/Qr\)). Saying that, we are still doing the same thing as given in the original formation of the normalized scattering intensity above. The difference here is we group distances falling into the same bin together, instead of calculating every single possible distance individually and explicitly. This is the fundamental reason why calculating the reciprocal space total scattering pattern following the Debye approach (see Eqn. 4.9 in the book by R. Neder and T. Proffen [2]) and the Fourier transform approach (as we will see next) should give very similar result (slight difference may pop up due to the difference between considering each pair explicitly and binning similar distances).
Furthermore, by defining a new function,
the function \(F(Q)\) can be further expressed as,
\[QF(Q) = \rho\int_{0}^{\infty}4\pi rG(r)sin(Qr)dr\]
from which one can clearly see that \(QF(Q)\) and \(rG(r)\) are linked by Fourier transform. Here we have the real version of Fourier transform, since the scattering measurement are measuring intensity only but not the phase and therefore we lose the phase information. Theoretically, accordance with such an experimental fact during our derivation for the scattering intensity dates back to Eqn. 6.22 in M. Dove’s book [1], where the square of the phase shift instead of the phase shift itself is used to reproduce the experimental scattering intensity.
As the partner equation of the one given just above, one has,
Here, the reason why we have \(1/(2\pi)^3\) term in the pre-factor is just that presented in early part of current blog. Specifically, the definition of \(Q\) is analogous to the angular frequency \(\omega\) we mentioned before, since we have \(Q = 2\pi/d\) where \(1/d\) is analogous to the frequency \(f\) we have before. Analogously, we can call \(1/d\) the space frequency and \(Q\) the space angular frequency. The cubic exponential in \(1/(2\pi)^3\) is coming from the fact that we have a 3D space and therefore naturally the factor \(1/2\pi\) should appear three times.
📌About maximum \(r\) or \(Q\)
Given a certain \(r\) or \(Q\) grid, one question one may ask is what is the corresponding maximum \(Q\) or \(r\) that we can reach - we know resolution in one space corresponds to the spanning range in the coupled space. However, how to quantify such a coupled relation is a question and this is to be covered next. Given the relation \(Q = 2\pi/d\), it may be straightforward to tell that \(Q_{range} = 2\pi/\Delta d\), where \(Q_{range}\) refers to the \(Q\)-space coverage range and \(\Delta d\) is the \(d\)-space interval between nearest points. However, this is INCORRECT and the CORRECT version should be,
Similarly one has,
\[d_{range} = \pi/\Delta Q\]where ‘range’ and \(\Delta\) carries the same meaning as mentioned above. So the question is, why do we miss the factor ‘2’ there? The fundamental reason for this is, in the Fourier transform space, alongside with the positive frequency, we also have the corresponding negative frequency and the negative frequency part is simply a mirror image of the positive part. Taking the Fourier transform from \(d\)- to \(Q\)-space as an example, the existence of mirroring to negative frequency means the actual \(Q\)-space coverage is \(2Q_{range}\) and therefore we cancel out the factor ‘2’ on both sides of the equation to give us \(Q_{range} = \pi/\Delta d\). So, next, we should spend a bit time to understand what negative frequency is and why we have it. Going back to the definition of Fourier transform presented above (e.g., the angular frequency case), we see that \(\hat{F}(\omega)\) is defined over the whole \(\mathcal{R}\) axis - this means definitely we will have negative frequency. Giving it a closer look, we have,
\[\begin{equation}\begin{aligned}\hat{F}(\omega) & = \int_{-\infty}^{\infty}f(x)e^{-i\omega x}dx\\ & = \int_{-\infty}^{\infty}f(x)cos(\omega x)dx - i\int_{-\infty}^{\infty}f(x)sin(\omega x)dx\\ & = A(\omega) - iB(\omega)\end{aligned}\nonumber\end{equation}\]When changing \(\omega\) to \(-\omega\), we know that \(cos\) function will not change while \(sin\) function will become negative. Therefore, we have,
\[\hat{F}(-\omega) = A(\omega) + iB(\omega)\]so that we know the positive and negative frequency is not independent which means in fact the negative frequency does not bring in anything new to our signal. So why do we still have negative frequency? Why don’t we change the definition domain for \(\hat{F}(\omega)\) to be \([0, \infty)\)? The reason is, with \(\hat{F}(\omega)\) being defined on the full \(\mathcal{R}\) axis, the inverse Fourier transform of \(\hat{F}(\omega)\) will give real function which has physical meaning (since simply the observable signal in practice should be real). To see this, we need to revisit the inverse Fourier transform,
\[f(x) = \frac{1}{2\pi}\int_{-\infty}^{\infty}\hat{F}(\omega)e^{ix\omega}d\omega\]where \(\hat{F}(\omega)\) is complex according to the definition of Fourier transform, and therefore, we can write,
\[\hat{F}(\omega) = |\hat{F}(\omega)|e^{i\phi(\omega)}\]where \(|\hat{F}(\omega)|\) and \(\phi(\omega)\) refers to the amplitude and phase of \(\hat{F}(\omega)\), respectively. So, the inverse Fourier transform can be written as,
\[\begin{equation}\begin{aligned}f(x) & = \frac{1}{2\pi}\bigg[\int_0^\infty\hat{F}(\omega)e^{ix\omega}d\omega + \int_{-\infty}^0\hat{F}(\omega)e^{ix\omega}d\omega\bigg]\\ & = \frac{1}{2\pi}\bigg[\int_0^\infty|\hat{F}(\omega)|e^{i[\phi(\omega) + x\omega]}d\omega + \int_{-\infty}^0|\hat{F}(\omega)|e^{i[\phi(\omega) + x\omega]}d\omega\bigg]\\ & = \frac{1}{2\pi}\bigg[\int_0^\infty|\hat{F}(\omega)|e^{i[\phi(\omega) + x\omega]}d\omega + \int_{\infty}^0|\hat{F}(-\omega_t)|e^{i[\phi(-\omega_t) - x\omega_t]}d(-\omega_t)\bigg]\\ & = \frac{1}{2\pi}\bigg[\int_0^\infty|\hat{F}(\omega)|e^{i[\phi(\omega) + x\omega]}d\omega + \int_0^\infty|\hat{F}(-\omega)|e^{i[\phi(-\omega) - x\omega]}d\omega\bigg]\\ & = \frac{1}{2\pi}\bigg[\int_0^\infty|\hat{F}(\omega)|e^{i[\phi(\omega) + x\omega]}d\omega + \int_0^\infty|\hat{F}(\omega)|e^{-i[\phi(\omega) + x\omega]}d\omega\bigg]\\ & =\frac{1}{2\pi}\int_0^\infty|\hat{F}(\omega)|\bigg[e^{i[\phi(\omega) + x\omega]} + e^{-i[\phi(\omega) + x\omega]}\bigg]d\omega\\ & = \frac{1}{2\pi}\int_0^\infty|\hat{F}(\omega)|cos[\phi(\omega) + x\omega]d\omega\end{aligned}\nonumber\end{equation}\]where we change the integration variable (\(\omega \rightarrow \omega_t\)) from line-2 to line-3. Using the fact that \(\omega_t\) is simply an integration dummy variable, we change it back to \(\omega\) and adjust the integration range accordingly (line-3 to line-4). From line-4 to line-5, we apply the relation between \(\hat{F}(\omega)\) and \(\hat{F}(\omega)\) – they have identical amplitude but opposite phase. From the result, we can see that by expanding the definition domain to include negative frequency, we can guarantee that the inverse Fourier transform will always give real result, which is exactly what we need in practice. As for the physical meaning of negative frequency, we can imagine the sinusoidal function pictorially as rotation - the positive and negative then just corresponds to the rotation in different directions, i.e. clockwise or counterclockwise.
References
[1] M. T. Dove, Structure and Dynamics: An Atomic View of Materials. Oxford University Press, New York, 2002.
[2] R. B. Neder and T. Proffen, Diffuse Scattering and Defect Structure Simulations, Oxford University Press, New York, 2008.