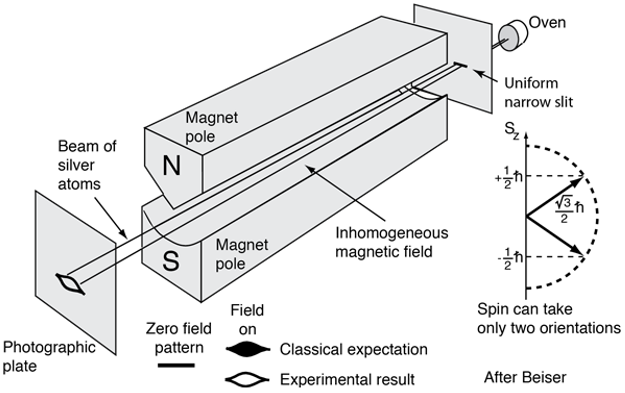
Illustration for Stern-Glach experiment [1].
Angular moment means rotation - this applies to electron as well. For electrons, any movement is associated with current and therefore angular moment naturally is tightly linked to current as well. Furthermore, current means magnetic field, as originated by Orsted. Mathematically, starting from expressing the current with the angular moment of rotating electrons, followed by detailed mathematics based on Biot-Savart law (induction \(\vec{B}\) as the function of current), one can arrive at the expression of magnetic induction in terms of magnetic (dipole) moment \(\vec{m}_l\). In another word, it can be shown that the magnetic field generated by electron rotation current is equivalent to that generated by magnetic dipole, with the equivalent dipole moment defined as (see Ref. [2] for detailed derivation),
\[\vec{m}_l = -\frac{1}{2}eR^2\vec{\omega}\]Given that the angular moment can be written as \(\vec{l} = m_eR^2\vec{\omega}\), we can obtain the following relation,
\[\vec{m}_l = -\frac{e}{2m_e}\vec{l}\]Defining the Bohr magneton as,
\[\mu_B := \frac{e\hbar}{2m_e}\]we arrive at the more familiar expression for the magnetic dipole moment,
\[\vec{m}_l = -\mu_B\frac{1}{\hbar}\]
This is what we mean by angular moment quantum number \(l\) in quantum mechanics. When we say the electron angular moment quantum number is 1, we mean, actually, \(l = \hbar\), as in the equation given above.
Everything now does not seem to be so strange yet - at least we can somehow start from classic mechanics to arrive at expression for quantum mechanics. However, things change a bit as we start to think about electron spin. Following the idea presented above, we know that electron spin should have similar expression as above for its corresponding effective magnetic dipole moment, i.e.
since anyways electron spin is indeed a sort of rotation, if we consider electron spin purely as classic phenomenon. However, in fact what we have is,
\[\vec{m}_s = -g\mu_B\frac{\vec{s}}{\hbar}\]where, if ignoring other effect (e.g. spin-orbital coupling), we would have \(g = 2\). But, where does the extra factor \(g\) comes from? Why do we need it? The reason is, if following the same format of the magnetic dipole moment expression, as for the orbital angular moment, we just have to have \(g = 2\) to have such a correspondence that \(g\vec{s} \sim \vec{l}\), since simply we have the spin quantum number for electron to be \(\frac{1}{2}\). But why do we have electron spin as one half? Why cannot we have electron spin quantum number as 1 so that we do not need to worry about the extra factor \(g\) at all? The reason goes way back to the Stern-Gerlach experiment, in which it was shown that the split of electron spin in magnetic filed is 2. In another word, we have two possible projections of spin onto the \(z\)-axis (the direction along the magnetic field). From the basic principle of quantum mechanics, we know that we have to have the electron spin quantum number to be \(\frac{1}{2}\) for such a splitting behavior of electron spin in magnetic field. More notes about this can be found in Ref. [3] - basically, the principle is the number of projections along the direction of magnetic field (our \(z\)-axis) should be \(2l + 1\), where we use \(l\) to represent angular moment in general.
N.B. \(l\) in quantum mechanics is usually used to represent orbital angular moment, but here we are using \(l\) to represent angular moment in general, i.e. it can refer to either orbital angular moment or electron spin angular moment.
References
[1] http://hyperphysics.phy-astr.gsu.edu/hbase/spin.html
[4] https://www.iris2020.net/2020/03/notes-on-magnetism-i-magnetism-of-free.html