In this post, some basics about the stray and demagnetization field will be covered. The post originates from reading the book by Stöhr – Ref. [1].
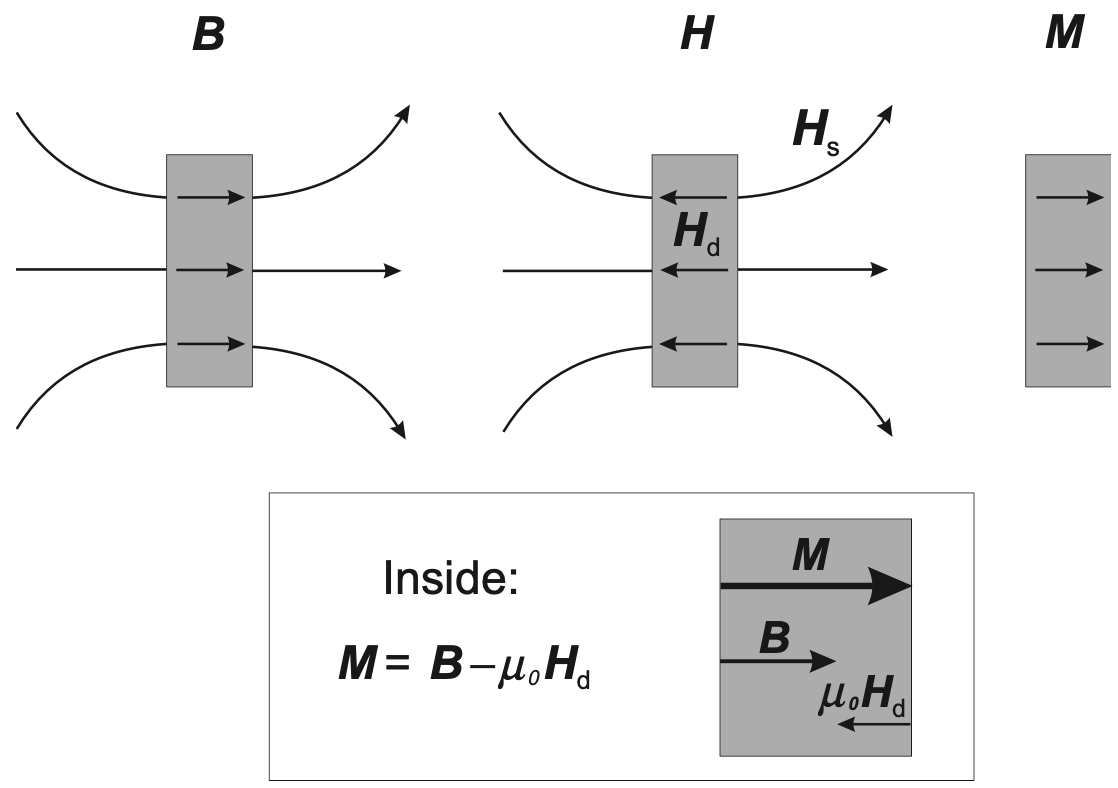
Figure. 1. Demonstration of materials magnetization – reproduced from Fig. 2.6 in Ref. [1].
To get an idea about the stray and demagnetization field, one needs to go back to the Stoke’s theorem,
\[\oint \vec{H} \cdot d\vec{l} = \iint_S (\nabla \times \vec{H})_n dS\]The integrand on the right hand side is the current density, according to,
\[\nabla \times \vec{H} = \vec{j}\]
In the case of no current flow, we have \(\vec{j} = 0\) and therefore we should accordingly have the left hand side being 0 as well. There then comes the requirement that we have the magnetic field inside and outside of the material being opposite to each other – inside the material, we have the demagnetization field (since it is opposite to the external magnetic field and therefore is trying to cancel it out) and outside the material, we have the stray field.
To get an idea about the relation between magnetization field inside the material and the magnetic field, one then needs to turn to the Gauss’s theorem,
\[\iint_S \vec{B} \cdot \vec{n} dS = \iiint_V \nabla \cdot \vec{B} dV\]Since we don’t have magnetic monopole, we should have the left hand side of the equation being 0, which then indicates \(\nabla \cdot \vec{B} = 0\).
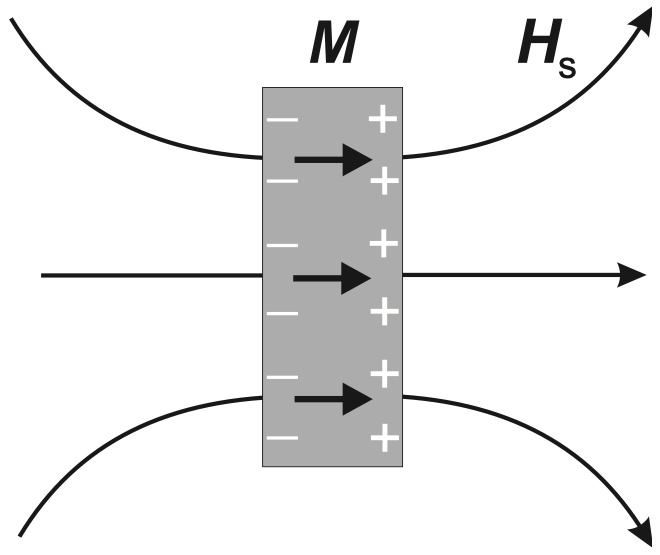
Figure. 2. Demonstration of materials magnetization – reproduced from Fig. 2.7 in Ref. [1].
Combined with the relation between magnetic induction field, magnetic field and magnetization field,
\[\vec{B} = \mu_0\vec{H} + \vec{M}\]we then have,
\[\mu_0\nabla \cdot \vec{H} = -\nabla \cdot \vec{M}\]
Mathematically, it is just a matter of reorganization of expression. However, physically, it infers a clear picture as presented in Fig. 2 – outside the material, it is just the stray field and inside the material, the end result of the interaction between the magnetic induction (\(\vec{B}\)) and the demagnetization (\(\vec{H}_d\)) field is the magnetization field (\(\vec{M}\)). Furthermore, we can imagine positive and negative magnetic ‘charge’ on the surface of the material, just like what we would have for electric field – though, in practice, we know that the magnetic ‘charge’ does not even exist. According to the equation above, we can say that the ‘positive charge’ on the right hand side of Fig. 2 is the source of the external stray field and is the sink of the internal magnetization field, and vice versa for the ‘negative charge’ on the left hand side.
N. B. In the equation above, when we say \(\vec{H}\), we mean both \(\vec{H}_d\) inside the material and \(\vec{H}_s\) outside the material.
References
[1] J. Stohr and H. C. Siegmann. Magnetism - from fundamentals to nanoscale dynamics. Springer. 2006. New York.